一. 冒泡排序的定义
冒泡排序(英语:Bubble Sort)是一种简单的排序算法。它重复地遍历要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
冒泡排序算法的运作如下: 1、比较相邻的元素。如果第一个比第二个大(升序),就交换他们两个。
2、对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
3、针对所有的元素重复以上的步骤,除了最后一个。
4、持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
二. 冒泡排序详细分析过程
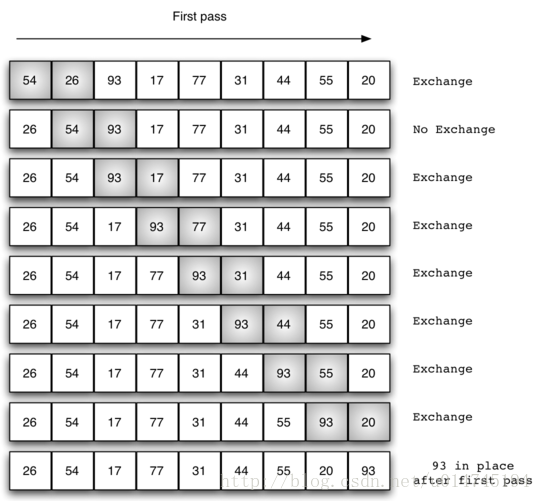
交换过程图示(第一次):
那么我们需要进行n-1次冒泡过程,每次对应的比较次数如下图所示
三. 冒泡排序时间复杂度
最优时间复杂度:O(n) (表示遍历一次发现没有任何可以交换的元素,排序结束。)
最坏时间复杂度:O(n^2)
稳定性:稳定
四. 冒泡排序的三种实现方法
def bubble(l): print l for index in range(len(l) - 1, 0 , -1): for two_index in range(index): if l[two_index] > l[two_index + 1]: l[two_index], l[two_index + 1] = l[two_index + 1], l[two_index] print l l = [10, 20, 40, 50, 30, 60]
方法1:就是依次遍历,把最小的数字沉到数组的最后
def bubble_improve(l): print l flag = 1 for index in range(len(l) - 1, 0 , -1): if flag: flag = 0 for two_index in range(index): if l[two_index] > l[two_index + 1]: l[two_index], l[two_index + 1] = l[two_index + 1], l[two_index] flag = 1 else: break print l l = [10, 20, 40, 50, 30, 60] bubble_improve(l)
方法2:就是加一个标志用来判断一次遍历的时候,还是否有交换,如果没有交换就说明已经排列好了,则退出;否则继续进行遍历。
def bubble_improve2(l): print l flag = 1 for index in range(len(l) - 1, 0 , -1): if flag: flag = 0 for two_index in range(index): flag_in = 0 if l[two_index] > l[two_index + 1]: l[two_index], l[two_index + 1] = l[two_index + 1], l[two_index] flag = 1 flag_in = 1 if flag_in: if two_index - 1 > 0: if l[two_index - 1] > l[two_index]: l[two_index - 1], l[two_index] = l[two_index], l[two_index - 1] else: break print l l = [10, 20, 40, 50, 30, 60] bubble_improve2(l)
方法2的变异,在一次移动之后和它之前的坐标相比较,如果符合条件就进行一次移动。
def bubble_improve1(l): print l flag = len(l) - 1 while(flag > 0): k = flag flag = 0 for j in range(k): if l[j] > l[j + 1]: l[j], l[j + 1] = l[j + 1], l[j] flag = j print l l = [10, 20, 40, 50, 30, 60] bubble_improve1(l)
方法3:也是 记录一个标志,这个标志是进行一次遍历的时候,最后交换的坐标,这样可以确定最后进行交换的位置,后面的就不需要再进行遍历了。
def bubble_improve(l): flag = 1 bottom = 0 top = len(l) - 1 while flag: flag = 0 for index in range(bottom, top, 1): if l[index] > l[index + 1]: l[index], l[index + 1] = l[index + 1], l[index] flag = 1 top = top - 1 for index in range(top, bottom, -1): if l[index] < l[index - 1]: l[index - 1], l[index] = l[index], l[index - 1] flag = 1 bottom = bottom + 1 print l l = [10, 20, 40, 50, 30, 60] bubble_improve(l)
-*- coding: utf-8 -*- def bubble_sort(alist): #结算列表的长度 n = len(alist) #外层循环控制从头走到尾的次数 for j in range(n - 1): #用一个count记录一共交换的次数,可以排除已经是排好的序列 count = 0 #内层循环控制走一次的过程 for i in range(0, n - 1 - j): #如果前一个元素大于后一个元素,则交换两个元素(升序) if alist[i] > alist[i + 1]: #交换元素 alist[i], alist[i + 1] = alist[i + 1], alist[i] #记录交换的次数 count += 1 count == 0 #代表没有交换,序列已经有序 if 0 == count: break if __name__ == '__main__': alist = [54, 26, 93, 77, 44, 31, 44, 55, 20] print("原列表为:%s" % alist) bubble_sort(alist) print("新列表为:%s" % alist) # 结果如下: # 原列表为:[54, 26, 93, 77, 44, 31, 44, 55, 20] # 新列表为:[20, 26, 31, 44, 44, 54, 55, 77, 93]
最常用的排序——快速排序
假设我们现在对“6 1 2 7 9 3 4 5 10 8”这个 10 个数进行排序。首先在这个序列中随便找一个数作为基准数(不要被这个名词吓到了,就是一个用来参照的数,待会你就知道它用来做啥的了)。为了方便,就让第一个数 6 作为基准数吧。接下来,需要将这个序列中所有比基准数大的数放在 6 的右边,比基准数小的数放在 6 的左边,类似下面这种排列。
3 1 2 5 4 6 9 7 10 8
在初始状态下,数字 6 在序列的第 1 位。我们的目标是将 6 挪到序列中间的某个位置,假设这个位置是 k。现在就需要寻找这个 k,并且以第 k 位为分界点,左边的数都小于等于 6,右边的数都大于等于 6。
分别从初始序列“6 1 2 7 9 3 4 5 10 8”两端开始“探测”。先从右往左找一个小于 6 的数,再从左往右找一个大于 6 的数,然后交换他们。这里可以用两个变量 i 和 j

首先哨兵 j 开始出动。因为此处设置的基准数是最左边的数,所以需要让哨兵 j 先出动,这一点非常重要(请自己想一想为什么)。哨兵 j 一步一步地向左挪动(即 j--),直到找到一个小于 6 的数停下来。接下来哨兵 i 再一步一步向右挪动(即 i++),直到找到一个数大于 6 的数停下来。最后哨兵 j 停在了数字 5 面前,哨兵 i 停在了数字 7 面前。


现在交换哨兵 i 和哨兵 j 所指向的元素的值。交换之后的序列如下。
6 1 2 5 9 3 4 7 10 8


到此,第一次交换结束。接下来开始哨兵 j 继续向左挪动(再友情提醒,每次必须是哨兵 j 先出发)。他发现了 4(比基准数 6 要小,满足要求)之后停了下来。哨兵 i 也继续向右挪动的,他发现了 9(比基准数 6 要大,满足要求)之后停了下来。此时再次进行交换,交换之后的序列如下。
6 1 2 5 4 3 9 7 10 8
第二次交换结束,“探测”继续。哨兵 j 继续向左挪动,他发现了 3(比基准数 6 要小,满足要求)之后又停了下来。哨兵 i 继续向右移动,糟啦!此时哨兵 i 和哨兵 j 相遇了,哨兵 i 和哨兵 j 都走到 3 面前。说明此时“探测”结束。我们将基准数 6 和 3 进行交换。交换之后的序列如下。
3 1 2 5 4 6 9 7 10 8



到此第一轮“探测”真正结束。此时以基准数 6 为分界点,6 左边的数都小于等于 6,6 右边的数都大于等于 6。回顾一下刚才的过程,其实哨兵 j 的使命就是要找小于基准数的数,而哨兵 i 的使命就是要找大于基准数的数,直到 i 和 j 碰头为止。
OK,解释完毕。现在基准数 6 已经归位,它正好处在序列的第 6 位。此时我们已经将原来的序列,以 6 为分界点拆分成了两个序列,左边的序列是“3 1 2 5 4”,右边的序列是“ 9 7 10 8 ”。接下来还需要分别处理这两个序列。因为 6 左边和右边的序列目前都还是很混乱的。不过不要紧,我们已经掌握了方法,接下来只要模拟刚才的方法分别处理 6 左边和右边的序列即可。现在先来处理 6 左边的序列现吧。
左边的序列是“3 1 2 5 4”。请将这个序列以 3 为基准数进行调整,使得 3 左边的数都小于等于 3,3 右边的数都大于等于 3。好了开始动笔吧。
如果你模拟的没有错,调整完毕之后的序列的顺序应该是。
2 1 3 5 4
OK,现在 3 已经归位。接下来需要处理 3 左边的序列“ 2 1 ”和右边的序列“5 4”。对序列“ 2 1 ”以 2 为基准数进行调整,处理完毕之后的序列为“1 2”,到此 2 已经归位。序列“1”只有一个数,也不需要进行任何处理。至此我们对序列“ 2 1 ”已全部处理完毕,得到序列是“1 2”。序列“5 4”的处理也仿照此方法,最后得到的序列如下。
1 2 3 4 5 6 9 7 10 8
对于序列“9 7 10 8”也模拟刚才的过程,直到不可拆分出新的子序列为止。最终将会得到这样的序列,如下。
1 2 3 4 5 6 7 8 9 10
到此,排序完全结束。细心的同学可能已经发现,快速排序的每一轮处理其实就是将这一轮的基准数归位,直到所有的数都归位为止,排序就结束了。下面上个霸气的图来描述下整个算法的处理过程。

快速排序之所比较快,因为相比冒泡排序,每次交换是跳跃式的。每次排序的时候设置一个基准点,将小于等于基准点的数全部放到基准点的左边,将大于等于基准点的数全部放到基准点的右边。这样在每次交换的时候就不会像冒泡排序一样每次只能在相邻的数之间进行交换,交换的距离就大的多了。因此总的比较和交换次数就少了,速度自然就提高了。当然在最坏的情况下,仍可能是相邻的两个数进行了交换。因此快速排序的最差时间复杂度和冒泡排序是一样的都是 O(N2),它的平均时间复杂度为 O(NlogN)。其实快速排序是基于一种叫做“二分”的思想。我们后面还会遇到“二分”思想,到时候再聊。
使用c代码实现:
#includeint a[101],n;//定义全局变量,这两个变量需要在子函数中使用 void quicksort(int left,int right) { int i,j,t,temp; if(left>right) return; temp=a[left]; //temp中存的就是基准数 i=left; j=right; while(i!=j) { //顺序很重要,要先从右边开始找 while(a[j]>=temp && i
可以输入以下数据进行验证
1061279345108
运行结果是
12345678910
下面是程序执行过程中数组 a 的变化过程,带下划线的数表示的已归位的基准数。
1 2 7 9 3 4 5 10 8 1 2 5 4 6 9 7 10 8 1 3 5 4 6 9 7 10 8 2 3 5 4 6 9 7 10 8 2 3 5 4 6 9 7 10 8 2 3 4 5 6 9 7 10 8 2 3 4 5 6 9 7 10 8 2 3 4 5 6 8 7 9 10 2 3 4 5 6 7 8 9 10 2 3 4 5 6 7 8 9 10 2 3 4 5 6 7 8 9 10
使用python实现快速排序的四种
1. 一行代码实现的简洁版本
quick_sort = lambda array: array if len(array) <= 1 else quick_sort([item for item in array[1:] if item <= array[0]]) + [array[0]] + quick_sort([item for item in array[1:] if item > array[0]])
2.常见的快排实现
def quick_sort(array, left, right): if left >= right: return low = left high = right key = array[low] while left < right: while left < right and array[right] > key: right -= 1 array[left] = array[right] while left < right and array[left] <= key: left += 1 array[right] = array[left] array[right] = key quick_sort(array, low, left - 1) quick_sort(array, left + 1, high)
由于快排是原地排序,因此不需要返回array。
array如果是个列表的话,可以通过len(array)求得长度,但是后边递归调用的时候必须使用分片,而分片执行的原列表的复制操作,这样就达不到原地排序的目的了,所以还是要传上边界和下边界的。
3.《算法导论》中的快排程序
def quick_sort(array, l, r): if l < r: q = partition(array, l, r) quick_sort(array, l, q - 1) quick_sort(array, q + 1, r) def partition(array, l, r): x = array[r] i = l - 1 for j in range(l, r): if array[j] <= x: i += 1 array[i], array[j] = array[j], array[i] array[i + 1], array[r] = array[r], array[i+1] return i + 1
这个版本跟上个版本的不同在于分片过程不同,只用了一层循环,并且一趟就完成分片,相比之下代码要简洁的多了。
4.用栈实现非递归的快排程序
一般意义上的栈有两层含义,一层是后进先出的数据结构栈,一层是指函数的内存栈,归根结底,函数的内存栈的结构就是一个后进先出的栈。汇编代码中,调用一个函数的时候,修改的也是堆栈指针寄存器ESP,该寄存器保存的是函数局部栈的栈顶,另外一个寄存器EBP保存的是栈底。不知道与栈存储空间相对的堆存储空间,其组织结构是否也是一个完全二叉树呢?
高级语言将递归转换为迭代,用的也是栈,需要考虑两个问题:
1)栈里边保存什么?
2)迭代结束的条件是什么?
栈里边保存的当然是需要迭代的函数参数,结束条件也是跟需要迭代的参数有关。对于快速排序来说,迭代的参数是数组的上边界low和下边界high,迭代结束的条件是low == high。
def quick_sort(array, l, r): if l >= r: return stack = [] stack.append(l) stack.append(r) while stack: low = stack.pop(0) high = stack.pop(0) if high - low <= 0: continue x = array[high] i = low - 1 for j in range(low, high): if array[j] <= x: i += 1 array[i], array[j] = array[j], array[i] array[i + 1], array[high] = array[high], array[i + 1] stack.extend([low, i, i + 2, high])